Среди выражений (−1)4; ![]() 40; (0,4)−1;
40; (0,4)−1; 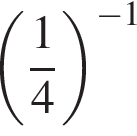 укажите то, значение которого равно 4.
укажите то, значение которого равно 4.
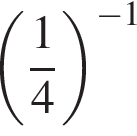
Среди выражений (−1)4; ![]() 40; (0,4)−1;
40; (0,4)−1; 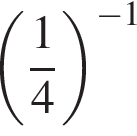 укажите то, значение которого равно 4.
укажите то, значение которого равно 4.
Общая стоимость 27 кг зефира составляет p руб. Укажите номер выражения, которое определяет цену (в рублях) одного килограмма зефира.
Если плоскость касается сферы, диаметр которой равен 12, то расстояние от центра сферы до точки касания равно:
Среди чисел −1; −2; −3; −5; −10 укажите то, которое является решением неравенства 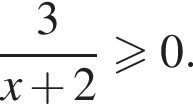
Укажите номер верного утверждения, если известно, что функция 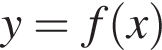 возрастает на множестве действительных чисел и
возрастает на множестве действительных чисел и 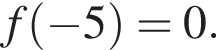
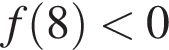

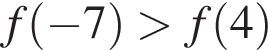
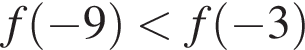
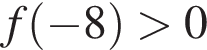
Укажите номера тех функций, которые являются нечетными.


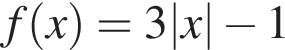
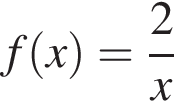
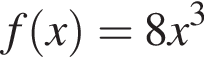
Площади двух участков поля находятся в отношении 4 : 7. Какова площадь (в гектарах) менышего участка поля, если общая площадь двух участков равна 495 га?
Найдите значение выражения 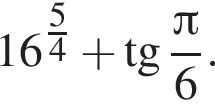
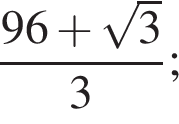
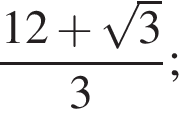
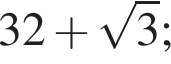

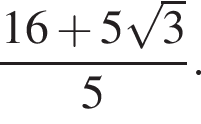
Прямая a пересекает плоскость α в точке A и образует с этой плоскостью угол 30°. Точка B лежит на прямой a, причем 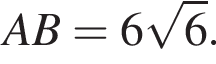 Найдите длину проекции отрезка AB на плоскость α.
Найдите длину проекции отрезка AB на плоскость α.
Укажите номера верных неравенств, если известно, что 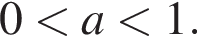
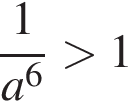
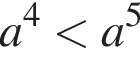

Для начала каждого из предложений А−В подберите его окончание 1−6 так, чтобы получилось верное утверждение.
A) Остаток при делении числа 526 на 3 равен ...
Б) Когда карандаши разложили в коробки по 4 штуки в каждую, то получилось 5 полных коробок и осталось 3 карандаша. Количество всех карандашей равно ...
В) Наибольшее натуральное число, которое при делении на 4 с остатком дает неполное частное, равное 7, равно ...
1) 12
2) 2
3) 31
4) 1
5) 32
6) 23
Oтвет запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
На рисунке изображены графики движения пяти мотоциклистов. Для начала каждого из предложений А−В подберите его окончание 1−5 так, чтобы получилось верное утверждение.
A) График движения мотоциклиста, который двигался с наименьшей скоростью, обозначен буквой ...
Б) График движения мотоциклиста, который двигался с наибольшей скоростью, обозначен буквой ...
В) График движения мотоциклиста, который двигался со скоростью 18 км/ч, обозначен буквой ...
1) A
2) B
3) C
4) D
5) F
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
Дан прямоугольный параллелепипед ABCDA1B1C1D1. Точки K и M лежат на ребрах A1B1 и DD1 соответственно, точка N лежит на прямой CC1 (см. рис.). Выберите верные утверждения:
1) прямая KN лежит в плоскости B1C1C;
2) прямая MN пересекает прямую C1D1;
3) прямая MN параллельна плоскости AA1B1;
4) прямая KM параллельна плоскости CBB1;
5) прямая KM лежит в плоскости KB1M;
6) прямая KM пересекает прямую B1C1.
Ответ запишите цифрами (порядок записи цифр не имеет значения). Например: 134.
Дана геометрическая прогрессия (bn), в которой b5 = −12, b6 = 36. Для начала каждого из предложений А−В подберите его окончание 1−6 так, чтобы получилось верное утверждение.
A) Знаменатель этой прогрессии равен ...
Б) Четвертый член этой прогрессии равен ...
В) Первый член этой прогрессии равен ...
1) −4
2) ![]()
3) ![]()
4) −3
5) 4
6) ![]()
Oтвет запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
Градусная мера угла ABC равна 126°. Внутри угла ABC проведен луч BD, который делит данный угол в отношении 1 : 6 (см. рис.). Найдите градусную меру угла 1, если BO — биссектриса угла DBC.
Найдите значение выражения 
Найдите значение выражения 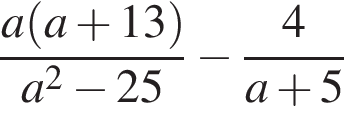 при
при 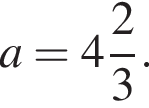
Верхнюю сторону листа фанеры прямоугольной формы разделили для покраски прямой линией на две части так, как показано на рисунке. Треугольную часть (I) покрасили краской белого цвета, а четырехугольную (II) — краской серого цвета. Сколько серой краски (в граммах) было использовано, если краски белого цвета понадобилось 270 г и расход краски (г/см2) обоих цветов одинаков?
Найдите значение выражения 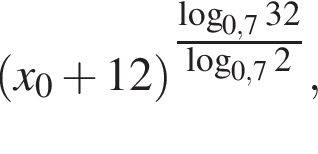 где x0 — корень уравнения
где x0 — корень уравнения 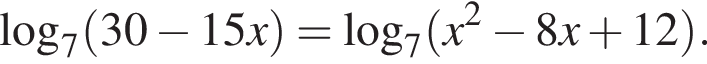
В равнобедренной трапеции диагональ перпендикулярна боковой стороне. Найдите значение выражения ![]() где S — площадь трапеции, если большее основание трапеции равно
где S — площадь трапеции, если большее основание трапеции равно ![]() а один из углов трапеции равен 60°.
а один из углов трапеции равен 60°.
На рисунке изображен график функции
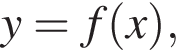 заданной на промежутке
заданной на промежутке 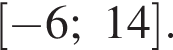 Найдите произведение значений аргумента, при которых
Найдите произведение значений аргумента, при которых 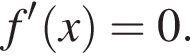 (Черными точками отмечены узлы сетки, через которые проходит график функции
(Черными точками отмечены узлы сетки, через которые проходит график функции 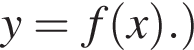
Найдите значение выражения 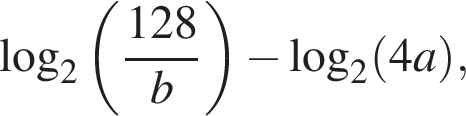 если
если 
Радиус основания цилиндра равен 13. Плоскость, параллельная оси цилиндра, пересекает цилиндр по прямоугольнику с площадью, равной 108. Найдите значение выражения ![]() где V — объем цилиндра, если расстояние от плоскости сечения до оси цилиндра равно
где V — объем цилиндра, если расстояние от плоскости сечения до оси цилиндра равно ![]()
Пусть (x1; y1), (x2; y2) — решения системы уравнений 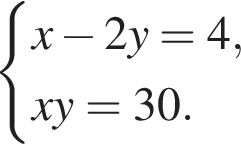 Найдите значение выражения
Найдите значение выражения 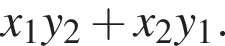
Найдите суму всех целых решений неравенства 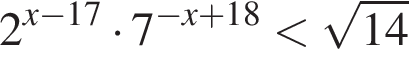 на промежутке (−25; 25).
на промежутке (−25; 25).
Многогранник ABCA1B1C1 — правильная треугольная призма, все ребра которой равны 6. Точки P и K — середины ребер B1C1 и CC1 соответственно, M ∈ AA1, A1M : A1A = 1 : 3 (см. рис.). Найдите увеличенный в 25 раз квадрат длины отрезка, по которому плоскость, проходящая через точки M, K, P, пересекает грань AA1B1B.
Найдите (в градусах) наименьший корень уравнения 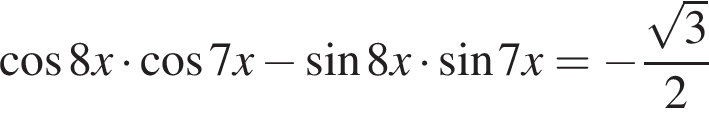 на промежутке
на промежутке 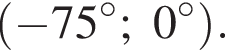
Найдите произведение корней уравнения 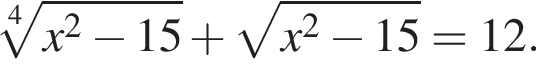
Два крана, работая одновременно, разгрузили баржу за 9 ч. Если бы половину баржи разгрузил первый кран, а затем оставшуюся часть — второй кран, то баржа была бы разгружена за 50 ч. За какое время (в часах) первый кран, работая один, разгрузил бы всю баржу, если известно, что он работает медленнее, чем второй кран?
ABCDA1B1C1D1 — куб. Точка K лежит на ребре AD куба так, что AK : KD = 1 : 4. Найдите значение выражения 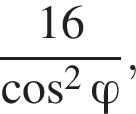 где φ — угол между прямыми D1K и A1C1.
где φ — угол между прямыми D1K и A1C1.